_ ＮＨＫの受信料

最近また話題なので雑談してみる。

引越しをしてテレビを設置された方はＮＨＫと受信契約をしてください。

ＮＨＫの素晴らしい放送は受信料によって成り立っています。

ただし以下の点に注意してください。

・一度契約すると解約できません。

・契約した後に不払いな人には法的手続きを取るそうです。

・集金に来るスタッフはＮＨＫの職員ではありません。

・集金人とは契約してはいけません。内容を書き換えられます。

・契約はＮＨＫの営業所で直接行いましょう。

・無理に断ると玄関を破壊したりしますので気をつけてやんわりと断りましょう。

・すぐにお帰り頂けない場合は警察を呼びましょう。来てくれませんが。

なんちゃって。

俺は当然ＮＨＫのアニメ大好きだったので過去に受信契約をした事があります。

地上波の受信設備しかなかったので「地上波カラー契約」をしてちょっとお得な銀行引き落としにしました。

しかし何故かＢＳ受信料を引き落とされた罠。

銀行で引き落としを停止し、ＮＨＫに何十回も電話してやっと過払い分を返してもらうことが出来ました。

昼間しか電話つながらないし、折り返すといいながら絶対返事無いし、あいつらもうどうしようもないです。

通信費は補償してもらえませんでしたが、交渉中に不払いにしていた１年分の受信料を免除させました。

こんな苦労するなら最初から契約しないほうがいいです。

という訳で今は受信契約してません。

テレビ無いし。

_ [日記][科学] エスカレーターは止まって利用したほうが効率的なのか？

エスカレーターの歩行利用は危険らしい。

確かに公共交通機関では健常者ばかりではないし、荷物がある人もいるので危険かもしれない。

ただ、混雑具合から「歩かない」ってのが非現実的な場面も通勤中にはあるような気がする。

どうせ駅員が押さないといけないような満員電車の時間帯なんかは立ち止まってたら返って危険な気もする。（人があふれて）

そんな中、「みんなが止まって利用したほうがむしろ効率が良い」という意見も耳にした。

たしかにそういう場面もある気がする。

気になったのでちょっと計算してみた。

＜仮定＞

だいたい毎分７０ステップくらいらしい。

なので以下のようにする。

■１分あたりに何人が新たに乗ることができるか＝平均サービス率μ

・止まって乗る場合

μ=70[人/分]

・歩く場合

μ=100[人/分]

移動速度は２倍近いとは思うが、すべてのステップに立てなくなると仮定して速度を少し落とした。

＊数字は片側のレーン。両側なら倍。

■１分間に平均何人到着するか＝平均到着時間λ

λ=９０人

■エスカレーターの長さN

N = 30ステップ分

＜理屈＞

まず、待ち行列をどのように仮定するかだが、情報処理試験などで良く出てくる[M/M/n]モデルを仮定する例が多いようだ。

[M/M/n]は、窓口n個に、ポアソン分布に従って何かが到着し、指数分布に従った処理時間で処理されるというモデルである。

簡単に言えば、ｎ個の窓口があって、そこにランダムに人が来て、ランダムの時間で用事を終えるというモデルである。

エスカレーターの場合、特に歩行しないで乗る場合にはステップに一人づつ立つという前提なので処理時間は指数分布ではないはずであるが・・・。

ま、とりあえずは検証のために[M/M/n]モデルで計算をしてみる。

まず両側に止まって立つ場合だが、[M/M/1]の待ち行列が２つあると考えるか、[M/M/2]の待ち行列として考えるかによって効率が異なる。

多くの場合は左右それぞれに列を作ってしまっているので[M/M/1]が妥当であろう。

[M/M/2]モデルでは窓口による処理時間のバラツキを効率化できるわけだが、今回のケースでは上記のようにあまり意味がない。

具体的には列の片方が偶然空いてしまうときに利用効率が著しく悪化するわけだが、現実的にそのような場合は人は列を移動するので発生しないはずである。

両側を歩行せずに利用する方法を＜止まって利用＞と呼ぶことにする。

一方、片側を歩行レーンとする場合は単純に二つの独立した窓口があると考えれば良い。

左右どちら側を歩行するかは地方によって異なるが、便宜的に左側を歩行しないレーン、右側を歩行レーンとする。

この例の場合、歩行したくない人と歩行したい人がどのくらいの割合で存在するかが結果に大きな影響を与える。

割合を１：１とした場合、両側を止まって使う場合に比べて、レーンごとの利用人数がちょうど同一となる。

つまり待ち時間は同一となるはずである。

片側を歩行レーンとする利用方法を＜歩行利用＞と呼ぶことにする。

最初の仮定を用いて計算した結果をグラフにすると以下のようになる。

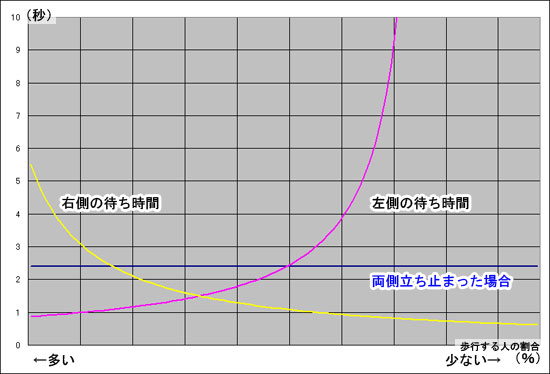
エスカレーターに乗るまでの待ち時間の比較

このグラフはエスカレーターに乗るまでの時間のみを示したもので、実際にエスカレーターの通過を終えるまでの時間はこの値にエスカレーターに乗っている時間を足したものになることを注意する。

（つまり、歩行レーンを歩いた人はすぐ到着するし、止まって乗った人はなかなか到着しない）

＜歩行利用＞では右側を歩く人の割合が少ないほど、左側の効率は大きく下がる。

具体的には左側に止まって乗る人の割合が５０％を超えると＜止まって利用＞に比べて待ち時間が増える。

この結果だけを見ると＜止まって利用＞の利用が安定して有利であるように見える。

ただし、このグラフはエスカレーターに乗るまでの時間のみを示したもので、実際にエスカレーターの通過を終えるまでの時間はこ　

の値にエスカレーターに乗っている時間を足したものになることに注意が必要である。

また、今回は比較的混雑した状況を想定したが、空いている場合は以下のようになる。

この例はλ＝２０とした場合の例である。（凡例は上のグラフと同じ）

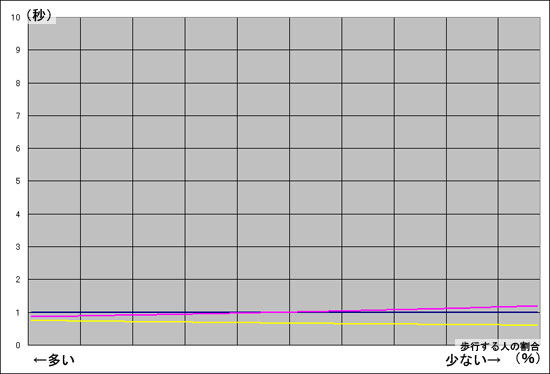
もう少し空いている状況のときのグラフ

わざと判りにくくしたわけじゃなくて、上とスケールを同じにしただけです・・。縦軸が（秒）なので、そもそも空いている時には待ち時間はほとんど存在しない。

この結果から、＜歩行利用＞と＜止まって利用＞の待ち時間の差はほとんどなく、＜歩行利用＞を許容すれば右側を歩行した人たち　

の所要時間が短くなり、かつ止まって利用する人の待ち時間もほとんど変わらないということがわかる。

逆にさらに混雑させた場合はどうであろうか？

λがエスカレーターの処理能力である７０を超えた場合、＜止まって利用＞では列をさばくことができなくなる。

つまり＜止まって利用＞の場合の平均待ち時間は無限大となる。

「＜止まって利用＞のほうがほとんどの人にとって効率的」という条件は結構狭いことがわかる。

ある程度空いている状況ではそもそも待ち時間がないし、ある程度混雑した場合は歩く人がいないと列が伸びる。

さて、ここまで来ておいてなんだが、やはり待ち行列のモデルがちょっとおかしいと思う。

上記で計算された待ち時間はどれも数秒であり、日常生活の経験からは待ち時間はもっと長いことがある。

といって、仮定よりも混雑したケースを想定すると待ち時間が無限大になってしまう。

この原因は人がエスカレーターのところにやってくる分布をポアソン分布で仮定したことにあると思う。

特に混雑するケースというのは駅のホームなどで電車が到着したタイミングなどである。

最近はもともと階段であったスペースをエスカレーターに置き換えてしまい、階段が存在しない通路もみられ、エスカレータに長い行列ができる。

＜仮定＞

n人が一気に到着し、全員がエスカレーターを利用する。

人数が二つの列に分かれるのでμは２倍。

最後まで処理する時間の半分が平均時間となるので２で除算する。

＜止まって利用＞

Tw= n / (μ×2) /2

Tw= 100/(140/60) /2 = 約21秒

平均待ち時間は約21秒。

＜歩行利用＞

[左]

TwL＝n/2 / μL /2

TwL = 100/2 /(70/60) /2 = 約21秒

平均待ち時間は約21秒。

[右]

μR

TwR＝n/2 / μL

TwR = 100/2 /(100/60) /2 = 約15秒

平均待ち時間は約15秒。

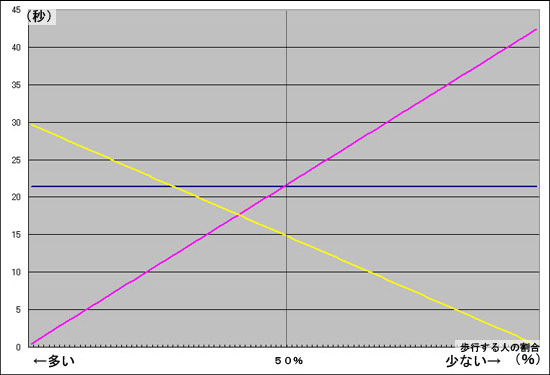
別のモデルの場合のグラフ

なんとも判断は難しいが、、

また、このグラフは「乗るまでの時間」であって、歩行した人の移動時間はかなり短縮され、かつ歩行しない人への待ち時間の影響　

もほとんど無い。

逆に言えば待ち時間に対する影響は＜歩行利用＞から＜止まって利用＞に変更してもさほど無いとも言える。

■まとめ

・歩行する人の割合が一定以下であり、かつ程好い混雑具合の場合は、「止まって乗る」ルールが有効。

　その条件はかなり狭いが、具体例をあげれば東京駅のJR線ホームへのエスカレーターは慢性的にそのような状況と個人的観測から　

推測する。

「止まったほうがみんな効率的」というのは、このような状況を見ての意見だと思われる。

これは、荷物を持った人が多く、長いエスカレーターで起こりやすいと考えられ、安全の面からも「止まって乗るルール」にすることが有効であると思われる。

・一方、一定以上に混雑した場面で、かつ歩行する人が一定数見込まれる場合は、片側歩行にした方がほとんどの人にとって効率が良い。

特に階段がないエスカレータのみ設置の駅のホームなどは顕著である。この場合、混雑が一定以上になると、歩行を許容しない場合は永遠に待ち行列が長くなり、転落事故になるだろう。

ただ、エスカレータを歩行することは近年、安全面から問題視する声が大きい。安易に階段をエスカレーターに置き換えず、階段を併設することが有効であると個人的には考える。

なお、「片側を歩くのはかえって非効率」というの意見は上記の結果から正しいとは言えないと思う。

この結果が成り立つ条件はかなり限定的である。

結局どうしたら良いのかは判らない。

通行量の多いにも関わらず安易に「歩行禁止」をうたって責任逃れしてもルールは守られず結局危険な状況を作ってしまう。

設置スペースが許す場所では、通路の全てをエスカレータにせず、階段の併設が良いと思う。エスカレーターに止まってのるより階段ほうが効率は良い。急ぐ人は階段を使えばいい。

または時間帯によってルールを変えることもひとつの解かもしれない。

■結論

・「やっぱり効率だけなら歩いたほうがパフォーマンスが良い」

・・・そして色々計算が面倒だったわりには結果がぱっとしない。。